DFAs recognize exactly the set of regular languages which are, among other things, useful for doing lexical analysis and pattern matching. [1] A DFA can be used in either an accepting mode to verify that an input string is indeed part of the language it represents, or a generating mode to create a list of all the strings in the language.
DFA is defined as an abstract mathematical concept, but due to the deterministic nature of DFA, it is implementable in hardware and software for solving various specific problems. For example, a software state machine that decides whether or not online user-input such as phone numbers and email addresses are valid. [2] Another example in hardware is the digital logic circuitry that controls whether an automatic door is open or closed, using input from motion sensors or pressure pads to decide whether or not to perform a state transition
A deterministic finite automaton M is a 5-tuple, (Q, Σ, δ, q0, F), consisting of
- a finite set of states (Q)
- a finite set of input symbols called the alphabet (Σ)
- a transition function (δ : Q × Σ → Q)
- a start state (q0 ∈ Q)
- a set of accept states (F ⊆ Q)
- r0 = q0
- ri+1 = δ(ri, ai+1), for i = 0, ..., n−1
- rn ∈ F.
A deterministic finite automaton without accept states and without a starting state is known as a transition system or semiautomaton.
For more comprehensive introduction of formal definition see automata theory.
A DFA representing a regular language can be used either in an accepting mode to validate that an input string is part of the language, or in a generating mode to generate a list of all the strings in the language.
In the accept mode an input string is provided which the automaton can read in left to right, one symbol at a time. The computation begins at the start state and proceeds by reading the first symbol from the input string and following the state transition corresponding to that symbol. The system continues reading symbols and following transitions until there are no more symbols in the input, which marks the end of the computation. If after all input symbols have been processed the system is in an accept state then we know that the input string was indeed part of the language, and it is said to be accepted, otherwise it is not part of the language and it is not accepted.
The generating mode is similar except that rather than validating an input string its goal is to produce a list of all the strings in the language. Instead of following a single transition out of each state, it follows all of them. In practice this can be accomplished by massive parallelism (having the program branch into two or more processes each time it is faced with a decision) or through recursion. As before, the computation begins at the start state and then proceeds to follow each available transition, keeping track of which branches it took. Every time the automaton finds itself in an accept state it knows that the sequence of branches it took forms a valid string in the language and it adds that string to the list that it is generating. If the language this automaton describes is infinite (ie contains an infinite number or strings, such as "all the binary string with an even number of 0s) then the computation will never halt. Given that regular languages are, in general, infinite, automata in the generating mode tends to be more of a theoretical construct
DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm to simulate a DFA on a stream of input. Given two DFAs there are efficient algorithms to find a DFA recognizing:
- the union of the two DFAs
- the intersection of the two DFAs
- complements of the languages the DFAs recognize
- whether a DFA accepts any strings
- whether a DFA accepts all strings
- whether two DFAs recognize the same language
- the DFA with a minimum number of states for a particular regular language
On the other hand, finite state automata are of strictly limited power in the languages they can recognize; many simple languages, including any problem that requires more than constant space to solve, cannot be recognized by a DFA. The classical example of a simply described language that no DFA can recognize is bracket language, that is, language that consists of properly paired brackets, such as (()()). More formally the language consisting of strings of the form anbn—some finite number of a's, followed by an equal number of b's. If there is no limit to recursion (i.e., you can always embed another pair of brackets inside) it would require an infinite amount of states to recognize.
A DFA represents a finite state machine that recognizes a RE. For example, the following DFA:
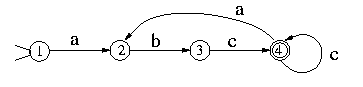
recognizes (abc+)+. A finite automaton consists of a finite set of states, a set of transitions (moves), one start state, and a set of final states (accepting states). In addition, a DFA has a unique transition for every state-character combination. For example, the previous figure has 4 states, state 1 is the start state, and state 4 is the only final state.
A DFA accepts a string if starting from the start state and moving from state to state, each time following the arrow that corresponds the current input character, it reaches a final state when the entire input string is consumed. Otherwise, it rejects the string.
A scanner based on a DFA uses the DFA's transition table as follows:
state = initial_state;
current_character = get_next_character();
while ( true )
{ next_state = T[state,current_character];
if (next_state == ERROR)
break;
state = next_state;
current_character = get_next_character();
if ( current_character == EOF )
break;
};
if ( is_final_state(state) )
`we have a valid token'
else `report an error'
This program does not explicitly take into account the longest match disambiguation rule since it ends at EOF. The following program is more general since it does not expect EOF at the end of token but still uses the longest match disambiguation rule. state = initial_state;
final_state = ERROR;
current_character = get_next_character();
while ( true )
{ next_state = T[state,current_character];
if (next_state == ERROR)
break;
state = next_state;
if ( is_final_state(state) )
final_state = state;
current_character = get_next_character();
if (current_character == EOF)
break;
};
if ( final_state == ERROR )
`report an error'
else if ( state != final_state )
`we have a valid token but we need to backtrack
(to put characters back into the input stream)'
else `we have a valid token'
Non-Deterministic Finite Automata:
In the theory of computation, a nondeterministic finite state machine or nondeterministic finite automaton (NFA) is a finite state machine where for each pair of state and input symbol there may be several possible next states. This distinguishes it from the deterministic finite automaton (DFA), where the next possible state is uniquely determined. Although the DFA and NFA have distinct definitions, it may be shown in the formal theory that they are equivalent, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction. Both types of automata recognize only regular languages. Non-deterministic finite state machines are sometimes studied by the name subshifts of finite type. Non-deterministic finite state machines are generalized by probabilistic automata, which assign a probability to each state transition.
Nondeterministic finite automata were introduced in 1959 by Michael O. Rabin and Dana Scott,[1] who also showed their equivalence to deterministic finite automata.
An NFA, similar to a DFA, consumes a string of input symbols. For each input symbol it transitions to a new state until all input symbols have been consumed.
Unlike a DFA, it is non-deterministic in that, for any input symbol, its next state may be any one of several possible states. Thus, in the formal definition, the next state is an element of the power set of states. This element, itself a set, represents some subset of all possible states to be considered at once.
An extension of the NFA is the NFA-lambda (also known as NFA-epsilon or the NFA with epsilon moves), which allows a transformation to a new state without consuming any input symbols. For example, if it is in state 1, with the next input symbol an a, it can move to state 2 without consuming any input symbols, and thus there is an ambiguity: is the system in state 1, or state 2, before consuming the letter a? Because of this ambiguity, it is more convenient to talk of the set of possible states the system may be in. Thus, before consuming letter a, the NFA-epsilon may be in any one of the states out of the set {1,2}. Equivalently, one may imagine that the NFA is in state 1 and 2 'at the same time': and this gives an informal hint of the powerset construction: the DFA equivalent to an NFA is defined as the one that is in the state q={1,2}. Transformations to new states without consuming an input symbol are called lambda transitions or epsilon transitions. They are usually labeled with the Greek letter λ or ε.
The notion of accepting an input is similar to that for the DFA. When the last input symbol is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.
Two similar types of NFAs are commonly defined: the NFA and the NFA with ε-moves. The ordinary is defined as a 5-tuple, (Q, Σ, T, q0, F), consisting of
- an initial (or start) state q0 ∈ Q
- a set of states F distinguished as accepting (or final) states F ⊆ Q.
Here, P(Q) denotes the power set of Q. The NFA with ε-moves (also sometimes called NFA-epsilon or NFA-lambda) replaces the transition function with one that allows the empty string ε as a possible input, so that one has instead
- T : Q × (Σ ∪{ε}) → P(Q).
It can be shown that ordinary NFA and NFA with epsilon moves are equivalent, in that, given either one, one can construct the other, which recognizes the same language.
The machine starts in the specified initial state and reads in a string of symbols from its alphabet. The automaton uses the state transition function T to determine the next state using the current state, and the symbol just read or the empty string. However, "the next state of an NFA depends not only on the current input event, but also on an arbitrary number of subsequent input events. Until these subsequent events occur it is not possible to determine which state the machine is in" [2]. If, when the automaton has finished reading, it is in an accepting state, the NFA is said to accept the string, otherwise it is said to reject the string.
The set of all strings accepted by an NFA is the language the NFA accepts. This language is a regular language.
For every NFA a deterministic finite state machine (DFA) can be found that accepts the same language. Therefore it is possible to convert an existing NFA into a DFA for the purpose of implementing a (perhaps) simpler machine. This can be performed using the powerset construction, which may lead to an exponential rise in the number of necessary states. A formal proof of the powerset construction is given here.
There are many ways to implement a NFA:
- Convert to the equivalent DFA. In some cases this may cause exponential blowup in the size of the automaton and thus auxiliary space proportional to the number of states in the NFA (as storage of the state value requires at most one bit for every state in the NFA)
- Keep a set data structure of all states which the machine might currently be in. On the consumption of the last input symbol, if one of these states is a final state, the machine accepts the string. In the worst case, this may require auxiliary space proportional to the number of states in the NFA; if the set structure uses one bit per NFA state, then this solution is exactly equivalent to the above.
- Create multiple copies. For each n way decision, the NFA creates up to n − 1 copies of the machine. Each will enter a separate state. If, upon consuming the last input symbol, at least one copy of the NFA is in the accepting state, the NFA will accept. (This, too, requires linear storage with respect to the number of NFA states, as there can be one machine for every NFA state.)
- Explicitly propagate tokens through the transition structure of the NFA and match whenever a token reaches the final state. This is sometimes useful when the NFA should encode additional context about the events that triggered the transition. (For an implementation that uses this technique to keep track of object references have a look at Tracematches [3].)
The following example explains a NFA M, with a binary alphabet, which determines if the input contains an even number of 0s or an even number of 1s. (Note that 0 occurrences is an even number of occurrences as well.) Let M = (Q, Σ, T, s0, F) where
- Σ = {0, 1},
- Q = {s0, s1, s2, s3, s4},
- E({s0}) = { s0, s1, s3 }
- F = {s1, s3}, and
M can be viewed as the union of two DFAs: one with states {S1, S2} and the other with states {S3, S4}.
Walang komento:
Mag-post ng isang Komento