Types Of Proofs

Proof by Construction:


In mathematics, a proof is a convincing demonstration (within the accepted standards of the field) that some mathematical statement is necessarily true.^[1][2] Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single exception. An unproven proposition that is believed to be true is known as a conjecture.
The statement that is proved is often called a theorem.^[1] Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as a lemma, especially if it is intended for use as a stepping stone in the proof of another theorem.
Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic. Purely formal proofs, written in symbolic language instead of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.

Proof by Contradiction:

In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition being false would imply a contradiction. Since by the law of bivalence a proposition must be either true or false, and its falsity has been shown impossible, the proposition must be true.
In other words, to prove by contradiction that P, show that or its equivalent . Then, since implies a contradiction, conclude P.
Proof by contradiction is also known as indirect proof, apagogical argument, reductio ad impossibile. It is a particular kind of the more general form of argument known as reductio ad absurdum.
A classic proof by contradiction from mathematics is the proof that the square root of 2 is irrational. If it were rational, it could be expressed as a fraction a/b in lowest terms, where a and b are integers, at least one of which is odd. But if a/b = √2, then a² = 2b². Therefore a² must be even. Because the square of an odd number is odd, that in turn implies that a is even. This means that b must be odd because a/b is in lowest terms.On the other hand, if a is even, then a² is a multiple of 4. If a² is a multiple of 4 and a² = 2b², then 2b² is a multiple of 4, and therefore b² is even, and so is b.So b is odd and even, a contradiction. Therefore the initial assumption—that √2 can be expressed as a fraction—must be false.
The method of proof by contradiction has also been used to show that for any non-degenerate Right triangle, the length of the hypotenuse is less than the sum of the lengths of the two remaining sides. The proof relies on the Pythagorean theorem. Letting c be the length of the hypotenuse and a and b the lengths of the legs, the claim is that a + b > c. As usual, we start the proof by negating the claim and assuming that a + b ≤ c. The next step is to show that this leads to a contradiction. Squaring both sides, we have (a + b)² ≤ c² or, equivalently, a² + 2ab + b² ≤ c². A triangle is non-degenerate if each edge has positive length, so we may assume that a and b are greater than 0. Therefore, a² + b² < a² + 2ab + b² ≤ c². Taking out the middle term, we have a² + b² < c². We know from the Pythagorean theorem that a² + b² = c². We now have a contradiction since strict inequality and equality are mutually exclusive. The latter was a result of the Pythagorean theorem and the former the assumption that a + b ≤ c. The contradiction means that it is impossible for both to be true and we know that the Pythagorean theorem holds. It follows that our assumption that a + b ≤ c must be false and hence a + b > c, proving the claim.
Proofs by contradiction sometimes end with the word "Contradiction!". Isaac Barrow and Baermann used the notation Q.E.A., for "quod est absurdum" ("which is absurd"), along the lines of Q.E.D., but this notation is rarely used today.^[1]

 A graphical symbol sometimes used for contradictions is a downwards zigzag arrow "lightning" symbol (U+21AF: ↯), for example in Davey and Priestley.^[2] Others sometimes used include a pair of opposing arrows (as or ), struck-out arrows (), a stylized form of hash (such as U+2A33: ⨳), or the "reference mark" (U+203B: ※).^[3][4] The "up tack" symbol (U+22A5: ⊥) used by philosophers and logicians (see contradiction) also appears, but is often avoided due to its usage for orthogonality.he method of proof by contradiction is to assume that a statement is not true and then to show that that assumption leads to a contradiction. In the case of trying to prove this is equivalent to assuming that That is, to assume that P is true and Q is false. This is known by its latin reductio ad absurdum (reduction to absurdity), since it ends with a statement that cannot be true.For many students, the method of proof by contradiction is a tremendous gift and a trojan horse, both of which follow from how strong the method is. In fact, the apt reader might have already noticed that both the constructive method and contrapositive method can be derived from that of contradiction.

Assume	Prove	Contradiction

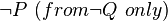However, its reach goes farther than even that, since the contradiction can be anything. Even if we ignore the criticisms from constuctivism, this broad scope hides what you lose; namely, you lose well-defined direction and conclusion, both of which have to be replaced with intuition.


Proof by Induction:

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers (non-negative integers). It is done by proving that the first statement in the infinite sequence of statements is true, and then proving that if any one statement in the infinite sequence of statements is true, then so is the next one.
The method can be extended to prove statements about more general well-founded structures, such as trees; this generalization, known as structural induction, is used in mathematical logic and computer science. Mathematical induction in this extended sense is closely related to recursion.
Mathematical induction should not be misconstrued as a form of inductive reasoning, which is considered non-rigorous in mathematics (see Problem of induction for more information). In fact, mathematical induction is a form of rigorous deductive reasoning.^[1]

An informal description of mathematical induction can be illustrated by reference to the sequential effect of falling dominoes.

In 370 BC, Plato's Parmenides may have contained an early example of an implicit inductive proof.^[2] The earliest implicit traces of mathematical induction can be found in Euclid's ^[3] proof that the number of primes is infinite and in Bhaskara's "cyclic method".^[4] An opposite iterated technique, counting down rather than up, is found in the Sorites paradox, where one argued that if 1,000,000 grains of sand formed a heap, and removing one grain from a heap left it a heap, then a single grain of sand (or even no grains) forms a heap.
An implicit proof by mathematical induction for arithmetic sequences was introduced in the al-Fakhri written by al-Karaji around 1000 AD, who used it to prove the binomial theorem and properties of Pascal's triangle.
None of these ancient mathematicians, however, explicitly stated the inductive hypothesis. Another similar case (contrary to what Vacca has written, as Freudenthal carefully showed) was that of Francesco Maurolico in his Arithmeticorum libri duo (1575), who used the technique to prove that the sum of the first n odd integers is n². The first explicit formulation of the principle of induction was given by Pascal in his Traité du triangle arithmétique (1665). Another Frenchman, Fermat, made ample use of a related principle, indirect proof by infinite descent. The inductive hypothesis was also employed by the Swiss Jakob Bernoulli, and from then on it became more or less well known. The modern rigorous and systematic treatment of the principle came only in the 19th century, with George Boole,^[5] Charles Sanders Peirce,^[6] Giuseppe Peano, and Richard Dedekind.^[4]

The simplest and most common form of mathematical induction proves that a statement involving a natural number n holds for all values of n. The proof consists of two steps:

1. The basis (base case): showing that the statement holds when n is equal to the lowest value that n is given in the question. Usually, n = 0 or n = 1.
2. The inductive step: showing that if the statement holds for some n, then the statement also holds when n + 1 is substituted for n.

The assumption in the inductive step that the statement holds for some n is called the induction hypothesis (or inductive hypothesis). To perform the inductive step, one assumes the induction hypothesis and then uses this assumption to prove the statement for n + 1.
The choice between n = 0 and n = 1 in the base case is specific to the context of the proof: If 0 is considered a natural number, as is common in the fields of combinatorics and mathematical logic, then n = 0. If, on the other hand, 1 is taken as the first natural number, then the base case is given by n = 1.
This method works by first proving the statement is true for a starting value, and then proving that the process used to go from one value to the next is valid. If these are both proven, then any value can be obtained by performing the process repeatedly. It may be helpful to think of the domino effect; if one is presented with a long row of dominoes standing on end, one can be sure that:

1. The first domino will fall
2. Whenever a domino falls, its next neighbor will also fall,

so it is concluded that all of the dominoes will fall, and that this fact is inevitable.